Hibridación y geometría molecular

Moléculas poliatómicas: hibridación de orbitales.

Considérese ahora la molécula de agua. La configuración electrónica del oxígeno es 2s2 2px2 2py1 2pz1. Los dos electrones de los orbitales 2py y 2pz pueden aparearse y formar enlaces σ con los orbitales 1s de los hidrógenos. Como estos orbitales p son perpendiculares entre sí, dichos enlaces σ deberían presentar esa misma separación. Sin embargo, el ángulo H-O-H es de 104.5º. Algo similar ocurre con la molécula de amoniaco. Los tres electrones de los orbitales p formarían sendos enlaces σ con los tres átomos de hidrógeno, y la separación también tendría que ser de 90º, cuando experimentalmente se conoce que dicho valor es de 107º. ¿Constituyen estas excepciones errores de la Teoría del Enlace de Valencia? Esta cuestión se resuelve a continuación.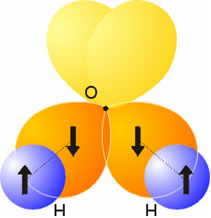

Explicación errónea de la molécula de agua.


Una deficiencia aparente de esta teoría es el no poder explicar la tetravalencia del carbono, es decir, su habilidad para formar cuatro enlaces. La configuración del átomo de carbono en su estado fundamental es 1s22s22px12py1, la cual sugiere que dicho átomo sólo puede formar dos enlaces en lugar de cuatro. Para que el carbono forme cuatro enlaces debe alcanzar su estado de valencia. El estado de valencia de un átomo en una molécula es el estado electrónico de ese átomo en el cual se puede combinar con los otros átomos para formar la molécula sin que sea necesaria ninguna reorganización electrónica adicional. Así pues, para que el C forme cuatro enlaces debe tener cuatro electrones en cuatro orbitales de la misma energía (estado V4), con los espines orientados al azar. Esos orbitales son los híbridos sp3.


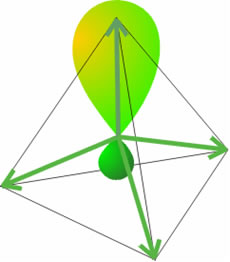
Orbitales híbridos sp3.


Así pues, para pasar del estado fundamental al estado de valencia es preciso promocionar un electrón del orbital 2s al 2p, y luego hibridar o mezclar los cuatro orbitales. La hibridación no es más que una mezcla o combinación lineal de orbitales atómicos puros (s y p, en este caso). La combinación lineal de un orbital 2s y de los tres orbitales 2p conduce a la formación de cuatro orbitales híbridos equivalentes:
h1 = s + px + py + pz
h2 = s – px + py – pz
h3 = s – px – py + pz
h4 = s – px – py – pz


Como resultado de esta interferencia entre los orbitales, cada orbital híbrido consiste en un lóbulo más abultado que el otro y que apunta directamente hacia un vértice de un tetraedro regular. El ángulo entre los orbitales híbridos corresponde a los ángulos de un tetraedro y tiene un valor de 109,4°. Como cada uno de estos orbitales híbridos se ha formado a partir de un orbital s y 3 orbitales p se denomina orbital híbrido sp3. Ahora resulta más sencillo describir la formación de la molécula AB4 desde el punto de vista de la Teoría del Enlace de Valencia. Cada uno de los orbitales híbridos que resultan tras la promoción en el átomo A contiene 1 electrón desapareado, que se aparea con el electrón que ocupa un orbital 1s de cada átomo de hidrógeno, originando un enlace σ que apunta hacia uno de los vértices de un tetraedro. Como cada orbital sp3 presenta la misma "composición", los cuatro híbridos son idénticos, salvo sus orientaciones en el espacio.


Existen otros tipos de orbitales híbridos que se emplean para explicar las geometrías de otras especies químicas mediante la teoría del enlace de valencia. Así, las combinaciones lineales de un orbital s con dos orbitales p conduce a los híbridos sp2 que sirven para explicar la geometría de las moléculas trigonales planas, como el BF3. La combinación lineal de un orbital s y uno p conduce a la formación de dos orbitales híbridos sp de geometría lineal. En la siguiente tabla se representan distintos tipos de orbitales híbridos y sus geometrías.

Orbitales híbridos y sus geometrías.

Número de coordinación	Distribución	Orbital híbrido
2	Lineal angular	sp, pd, sd sd
3	Plana triangular Pirámide trigonal	sp2, p2d pd2
4	Tetraedro Plana cuadrada	sp3, sd3 p2d2, sp2d
5	Bipirámide trigonal Pirámide tetragonal Plana pentagonal	sp3d, spd3 sp2d2, sd4, pd4, p3d2 p2d3
6	Octaedro	p3d2

Teoria de Orbitales Moleculares

La Teoría de Orbitales Moleculares (T.O.M.) es la segunda aproximación al estudio del enlace covalente, y la más ampliamente empleada para explicar la estructura y la geometría de muchos sólidos inorgánicos. El punto de partida consiste en asumir que si los dos núcleos implicados en el enlace se ubican a la distancia de equilibrio, los electrones se alojarán no en orbitales atómicos de cada elemento, sino en orbitales moleculares, que son análogos a los atómicos, y que presentan características similares, como se verá más adelante. Esta analogía es de tal grado que al igual que ocurría con los átomos polielectrónicos, no es posible resolver la ecuación de Schrödinger de forma exacta para la molécula, y de nuevo hay que recurrir a métodos aproximados para conocer la forma de las funciones de onda que representen los mencionados orbitales moleculares.


Uno de los métodos más empleados es el que hace uso de las Combinaciones Lineales de Orbitales Atómicos (CLOA). Esta aproximación puede entenderse de forma simple si se piensa que cuando un electrón esté cerca de uno de los núcleos, es decir, cuando esté “controlado” por un núcleo, su función de onda será muy similar a la de un orbital atómico. Los orbitales moleculares de la molécula de H2 se obtienen de forma aproximada mediante la combinación lineal de los orbitales atómicos 1s de cada átomo de hidrógeno. Únicamente se pueden escribir dos combinaciones lineales:


Ψ+ = cAφA +cBφB
Ψ- = cAφA – cBφB


Los coeficientes ci que aparecen en la combinación lineal reflejan la contribución de cada orbital atómico al orbital molecular: cuanto mayor sea el valor del coeficiente mayor será la participación del orbital atómico en el molecular. Para la molécula de H2 la contribución de ambos orbitales atómicos a los orbitales moleculares es la misma, esto es, cA = cB = 1, de forma que las expresiones matemáticas de las funciones de onda se pueden simplificar:


Ψ+ = φA + φB
Ψ- = φA – φB
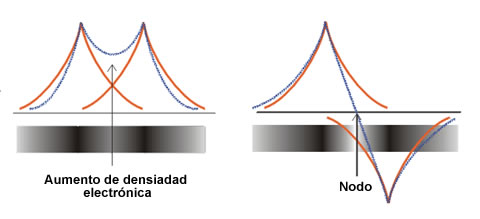Ψ + (izquierda) y Ψ- (derecha)


En la figura anterior se representan las funciones Ψ+ y Ψ- (parte radial) frente a la distancia internuclear. La función Ψ+ concentra la densidad electrónica entre los dos núcleos, debido a una interferencia constructiva φA y φB, lo que aumenta la amplitud en la región internuclear. Por el contrario, la función de onda Ψ- concentra la densidad electrónica fuera de la zona comprendida entre los dos núcleos. La interferencia de tipo destructivo entre las funciones de onda φA y φBcancela sus amplitudes y da lugar a la formación de un plano nodal en la región internuclear. Obviamente, la molécula será más estable si los electrones se encuentran en el orbital Ψ+, porque esto origina un aumento de la atracción electrón-núcleo y una disminución de las repulsiones nucleares. La combinación Ψ+ = φA + φB corresponde al orbital molecular de menor energía y se denomina orbital molecular enlazante, que ahora se representa como Ψe. Por el contrario, la combinación Ψ- = φA – φB, representa al orbital molecular de mayor energía denominado orbital molecular antienlazante (Ψa). Las energías relativas de los dos orbitales moleculares se muestran en la siguiente figura, que constituye un ejemplo de lo que se conoce como Diagrama de Orbitales Moleculares o Diagrama de Niveles de Energía.


De forma análoga a las limitaciones en el caso de átomos, el principio de exclusión de Pauli limita a dos el número de electrones que pueden ocupar un orbital molecular, lo que obliga a su apareamiento. La molécula de H2 posee una energía menor que los dos átomos de H por separados porque los dos electrones ocupan el orbital molecular enlazante y ambos contribuyen a una disminución de la energía del sistema.

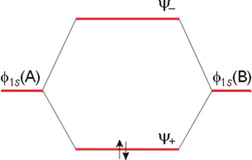
Diagrama de Orbitales Moleculares de la molécula de Hidrógeno.


En definitiva, el enlace en la molécula de hidrógeno puede ahora explicarse en función de la formación de dos orbitales moleculares a partir de dos orbitales atómicos. De forma general, N orbitales atómicos pueden conducir a la formación de N orbitales moleculares. Los electrones ocuparán los Orbitales moleculares siguiendo las mismas reglas que las especificadas para las configuraciones electrónicas de los elementos.

Enlace iónico

El enlace iónico consiste en la atracción electrostática entre átomos con cargas eléctricas de signo contrario. Este tipo de enlace se establece entre átomos de elementos poco electronegativos con los de elementos muy electronegativos. Es necesario que uno de los elementos pueda ganar electrones y el otro perderlo, y como se ha dicho anteriormente este tipo de enlace se suele producir entre un no metal (electronegativo) y un metal (electropositivo).


Un ejemplo de sustancia con enlace iónico es el cloruro sódico. En su formación tiene lugar la transferencia de un electrón del átomo de sodio al átomo de cloro. Las configuraciones electrónicas de estos elementos después del proceso de ionización son muy importantes, ya que lo dos han conseguido la configuración externa correspondiente a los gases nobles, ganando los átomos en estabilidad. Se produce una transferencia electrónica, cuyo déficit se cubre sobradamente con la energía que se libera al agruparse los iones formados en una red cristalina que, en el caso del cloruro sódico, es una red cúbica en la que en los vértices del paralelepípedo fundamental alternan iones Cl- y Na+. De esta forma cada ion Cl-queda rodeado de seis iones Na+ y recíprocamente. Se llama índice de coordinación al número de iones de signo contrario que rodean a uno determinado en una red cristalina. En el caso del NaCl, el índice de coordinación es 6 para ambos

Propiedades de los compuestos iónicos

Las sustancias iónicas están constituidas por iones ordenados en el retículo cristalino; las fuerzas que mantienen esta ordenación son fuerzas de Coulomb, muy intensas. Esto hace que las sustancias iónicas sean sólidos cristalinos con puntos de fusión elevados. En efecto, para fundir un cristal iónico hay que deshacer la red cristalina, separar los iones. El aporte de energía necesario para la fusión, en forma de energía térmica, ha de igualar al de energía reticular, que es la energía desprendida en la formación de un mol de compuesto iónico sólido a partir de los correspondientes iones en estado gaseoso. Esto hace que haya una relación entre energía reticular y punto de fusión, siendo éste tanto más elevado cuanto mayor es el valor de aquella.


Por otra parte, la aparición de fuerzas repulsivas muy intensas cuando dos iones se aproximan a distancias inferiores a la distancia reticular (distancia en la que quedan en la red dos iones de signo contrario), hace que los cristales iónicos sean muy poco compresibles. Hay sustancias cuyas moléculas, si bien son eléctricamente neutras, mantienen una separación de cargas. Esto se debe a que no hay coincidencia entre el centro de gravedad de las cargas positivas y el de las negativas: la molécula es un dipolo, es decir, un conjunto de dos cargas iguales en valor absoluto pero de distinto signo, separadas a una cierta distancia. Los dipolos se caracterizan por su momento; producto del valor absoluto de una de las cargas por la distancia que las separa. Un de estas sustancias polares es, por ejemplo el agua.


Cuando un compuesto iónico se introduce en un disolvente polar, los iones de la superficie de cristal provocan a su alrededor una orientación de las moléculas dipolares, que enfrentan hacia cada ion sus extremos con carga opuesta a la del mismo. En este proceso de orientación se libera una energía que, si supera a la energía reticular, arranca al ion de la red. Una vez arrancado, el ion se rodea de moléculas de disolvente: queda solvatado. Las moléculas de disolvente alrededor de los iones se comportan como capas protectoras que impiden la reagrupación de los mismos. Todo esto hace que, en general, los compuestos iónicos sean solubles en disolventes polares, aunque dependiendo siempre la solubilidad del valor de la energía reticular y del momento dipolar del disolvente. Así, un compuesto como el NaCl, es muy soluble en disolventes como el agua, y un compuesto como el sulfato de bario, con alta energía reticular, no es soluble en los disolventes de momento dipolar muy elevado.

3.3.2 Redes cristalinas

Las estructuras de los sólidos

IntroducciónLa característica principal de un sólido, ya sea metálico o ionico, es la disposición de sus átomos e iones que conducen a la formación del cristal. En estas sustancias no existe un enlace covalente direccional predominante, sino que cada uno de los átomos se considera enlazado al resto del cristal. Esta disposición suele representarse por medio de esferas sólidas. Un cristal de un elemento o de un compuesto puede considerarse, desde el punto de vista formal de su construcción, como la repetición regular de unidades asimétricas, que pueden ser átomos, moléculas o iones. Esa unidad se denomina celda unidad. La Figura 1 muestra un ejemplo de celda unidad para una sólido bidimensional. Las dos unidades que aparecen sombreadas representan sendas celdas unidades, ya que su traslado a lo largo del plano conduce a la formación de la red. Sin embargo, suele emplearse como celda unidad aquella de más alta simetría y de menor tamaño, lo que en este caso sucede para (a).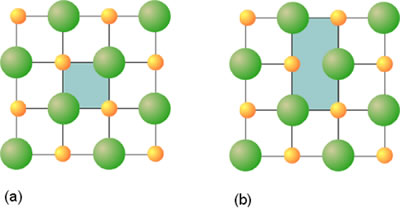



Figura 1. Celda unidad para un sólido bidimensional.

La mayoría de sólidos metálicos e iónicos están formados por átomos o iones que desde un punto de vista práctico pueden considerarse como esferas. Sin la existencia de enlace covalente direccional, estas esferas podrían empaquetarse de forma tan compacta como permitiera la geometría, de forma que el espacio que no se ocupara entre ellas sea el mínimo. Esto es lo que se denomina empaquetamiento compacto. En esta situación, y cuando se trata de átomos idénticos, cada esfera está directamente rodeada por doce esferas vecinas. Este número se denomina número de coordinación.
Empaquetamiento de esferas

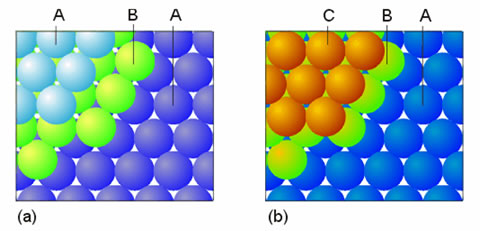
Figura 2. Los dos politipos de empaquetamiento compacto. (a) Hexagonal, (b) Cúbico

La formación de estructuras compactas puede visualizarse de manera simple. La primera capa consiste en esferas tangentes entre sí de tal forma que cada una de ellas está rodeada de otras seis en dicha capa. La segunda capa se construye ubicando las esferas sobre los puntos de tangencia de las esferas de la primera capa. Es en la formación de la tercera capa donde surgen diferencias, que conducen a la formación de politipismo: estructuras idénticas en dos dimensiones pero distintas en la tercera. El número de coordinación es el mismo (12) en ambos politipos.

Empaquetamiento Compacto

Uno de los politipos se forma cuando las esferas de la tercera capa ocupan posiciones sobre las esferas de la primera, en lo que se denomina estructura ABAB..., donde A representa una capa y B representa otra capa (Figura 2a). Esto supone la aparición de una celda unidad hexagonal (Figura 3 a), por lo que se denomina empaquetamiento compacto hexagonal. El segundo politipo se forma cuando las esferas de la tercera capa ocupan posiciones sobre los huecos que se forman en la primera capa (Figura 2b). En este caso la disposición conduce a una distribución ABCABC..., lo que indica que hay tres tipos de capas en lo que a su ubicación respectiva se refiere. La celda unidad correspondiente presenta simetría cúbica (Figura 3b), lo que explica su denominación: empaquetamiento cúbico compacto.

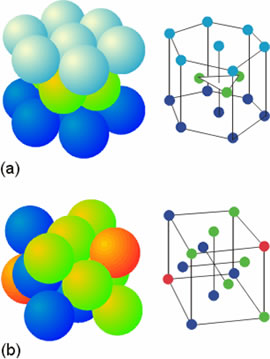
Figura 3. Celdas unidad de los empaquetamientos compactos hexagonal (a) y cúbico (b).

Huecos en estructuras empaquetadasUna de las características de los empaquetamientos es el tipo de huecos que se genera entre las esferas. Para una estructura compacta, la porción de espacio no ocupada, es decir, la cantidad de espacio libre por huecos, es el 26 % del total. Existentes dos tipos de huecos: el hueco octaédrico y el hueco tetraédrico.
El hueco octaédrico aparece entre dos triángulos de esferas que están opuestos entre sí (Figura 4). En una estructura compacta de N átomos existen N huecos octaédricos. Además, cada hueco presenta simetría octaédrica, ya que los seis átomos que lo forman se disponen en los vértices de un octaedro (Figura 4). Si cada esfera tiene un radio r, puede demostrarse fácilmente que un hueco de estas características puede acomodar otra esfera de radio 0.414r.

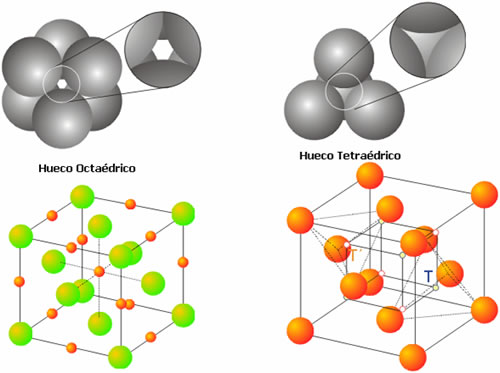
Figura 4. Huecos Octaédricos y Tetraédricos

El hueco tetraédrico aparece como consecuencia de la ubicación de una esfera sobre el triángulo que forman otras tres (Figura 4). Existen dos tipos de agujeros tetraédricos, dependiendo de que el vértice del mismo está orientado hacia arriba o hacia abajo (Figura 4). En un empaquetamiento compacto existen N huecos de cada tipo, para dar un total de 2N huecos tetraédricos. En una estructura de este tipo, con átomos de radio r, el hueco tetraédrico puede acomodar una esfera de radio igual o inferior a 0.225r.